Integration by substitution (tutorial)
Tutorial: Integration by substitution
 Throughout this tutorial you will often see the Leibniz notation for derivatives and differentials, named after the German mathematician Gottfried Wilhelm Leibniz (1646-1716). The beauty of this notation is that it provides an easy way to remember several important calculus formulas by making it seem as though the formulas were derived from algebraic manipulations of differentials. For instance, in Leibniz notation, the rule for differentiating a composite function – often referred to as the Chain Rule – is written as .
Throughout this tutorial you will often see the Leibniz notation for derivatives and differentials, named after the German mathematician Gottfried Wilhelm Leibniz (1646-1716). The beauty of this notation is that it provides an easy way to remember several important calculus formulas by making it seem as though the formulas were derived from algebraic manipulations of differentials. For instance, in Leibniz notation, the rule for differentiating a composite function – often referred to as the Chain Rule – is written as .
This statement appears to be true because the du’s cancel. Even though this reasoning is theoretically incorrect, it is reasonable to consider that differentials such as dx and dy represent infinitesimally small numbers so in practice differentials can be manipulated using the rules of algebra.
In fact, the formula booklets for IB Maths HL & SL express the Chain Rule as follows.
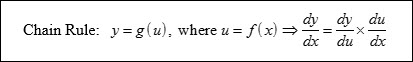
The following is a formal definition of the Chain Rule that one may find in a standard calculus textbook.

Using the Chain Rule
Example 1: Find for .
Explanation/Solution:
For this function, you can consider the “inside” function to be and the “outside” function to be . Hence, . Then by the Chain Rule, you obtain and since then .
Questions 1 - 5
Find the derivative of each function:
| 1. | 2. | 3. |
| 4. | 5. |
Answers for Qs 1-5
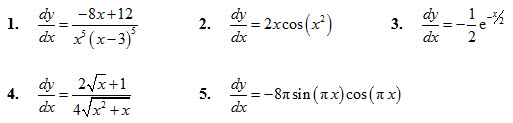
Differentiation and integration are inverse operations. Hence, a good starting point for investigating a particular integration method is to rewrite a differentiation rule backwards.
Integration by Substitution
The role of substitution in integration is comparable to the role of the Chain Rule in differentiation. For differentiable functions given by , the Chain Rule states that
or, alternatively
Working backwards and letting , i.e. F is the antiderivative of f, it follows that
If , then and
Note that in the integral , the integrand is a composite function made up of an “outside” function f and an “inside” function g. Also the derivative of the “inside” function, , is a factor of the integrand.
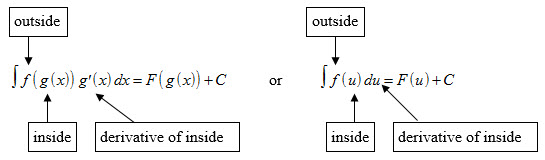
Using Integration by Substitution
In order to apply this technique of integration – essentially performing the Chain Rule backwards – one must recognize a pattern in the integrand as illustrated above. If the integrand follows the pattern (can also be represented by ), then it will be possible to apply integration by substitution – which usually involves performing a u-substitution. This change of variable technique uses the Leibniz notation for the differential. That is, if and then the integral takes the form:
(recall that F is the antiderivative of f )
Example 2: Evaluate
Explanation/Solution:
Let u be the “inside” function, ; then . Substitute to obtain the following:
Now continue by finding the antiderivative F of
re-substituting gives
Question 6
Use the Chain Rule to verify that the derivative of is the integrand of the original integral in Example 2.
Answer for Q 6
Many integrands contain the essential part (i.e. the variable part) of du, but are missing a constant multiple. In such cases, one can multiply and divide by the necessary constant multiple.
Example 3: Evaluate
Explanation/Solution:
This is similar to the integral in Example 2, except that the integrand is missing a factor of 2. Recognizing that 2x is the derivative of , you can let and since then it follows that and then substituting gives the following:
Example 4: Evaluate
Explanation/Solution:
The key recognition is that and that the derivative of is very close (only off by a constant) to . Therefore, let and . Substituting and in the given integral gives the following:
Question 7
Verify the result for Example 4 above by finding the derivative of .
When using u-substitution with a definite integral (examples 2 – 4 were indefinite integrals), it is often convenient to determine the limits of integration for the variable u rather than to convert the antiderivative back to the variable x and evaluate at the original limits. Symbolically, this can be expressed as
Example 5 below illustrates this.
Answer for Q 7
Example 5: Evaluate
Explanation/Solution:
Let
Before substituting, determine the new upper and lower limits of integration.
lower limit: when upper limit:
Now, you can substitute to obtain
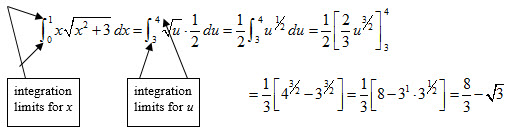
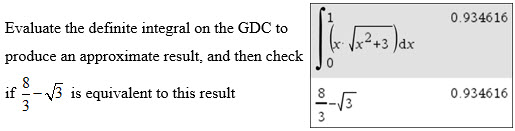
Question 8
Explain how you can check the result for Example 5 above using your GDC.
Answer for Q 8
Questions 9 & 10
Evaluate each integral in two different ways. Explain any difference in the forms of the answers.
9. 10.
Answers for Qs 9 & 10

Questions 11-14
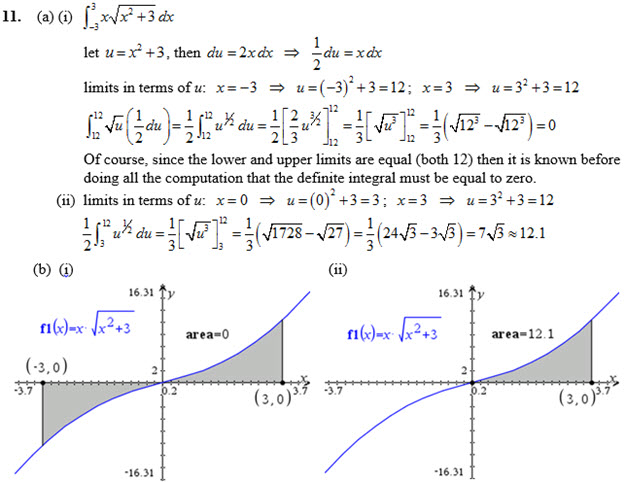
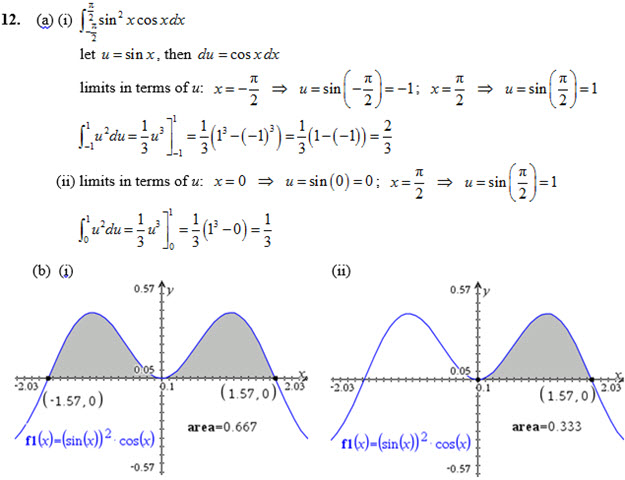
For each definite integral: (a) Evaluate for two different sets of limits: (i) from ; and (ii) from . Evaluate the definite integrals by u-substitution and integrate with limits for u (as in Example 5). (b) Verify each answer by graphing the function on your GDC and evaluating the definite integral on your GDC.
11. 12.
13. 14.
Answer for Q 11
Answer for Q 12
Answer for Q 13
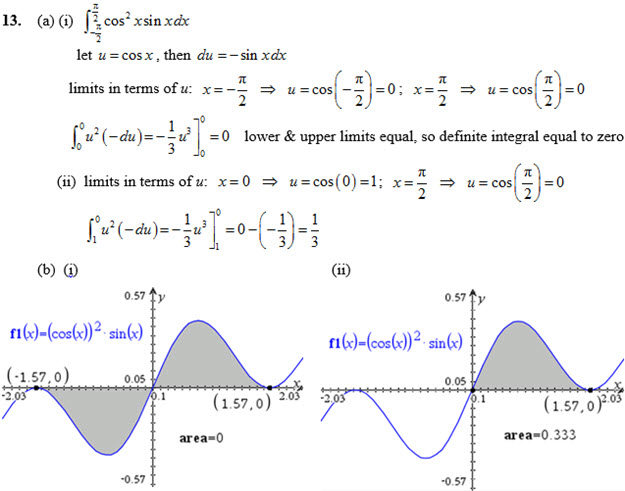
Answer for Q 14
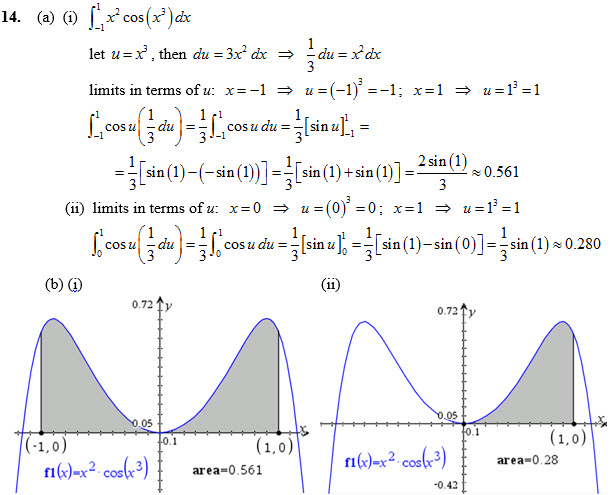
Question 15
From your work on questions 11 – 14, form some conclusions/conjectures regarding definite integrals and the symmetry of certain types of functions.
Answer for Q 15

Question 16
Find an equation for the function f that has the indicated derivative and whose graph passes through the given point.
Answer for Q 16
Questions 17-22
Determine whether the statement is true or false. If it is true, show mathematical working and/or reasoning to verify the statement; and if it is false, explain why or give an example that shows it is false.
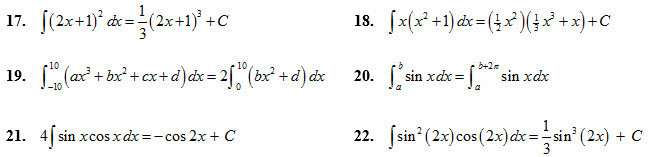
Answers for Qs 17-19
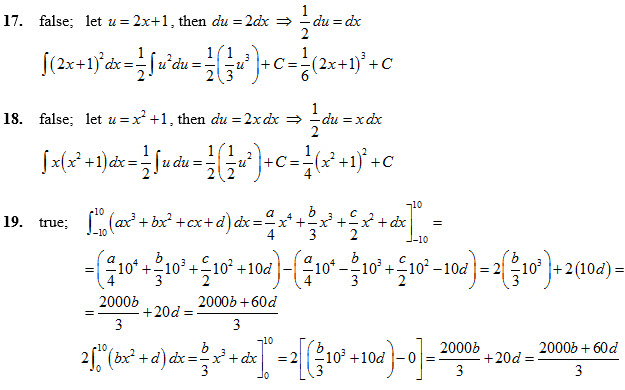
Answers for Qs 20-22
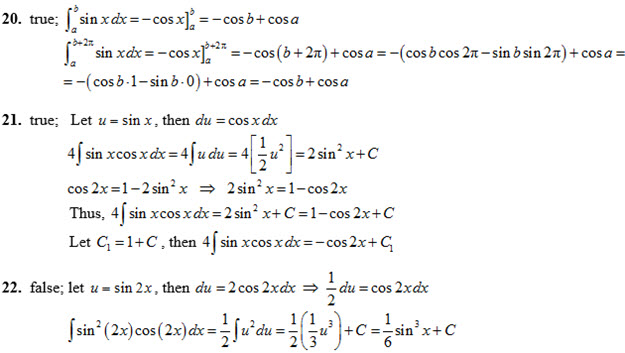
download tutorial here:

 IB Docs (2) Team
IB Docs (2) Team
